我偷偷生成一波数据$x$,生成1000个吧,这些数据是从一个分布取样的,既然是偷偷生成的,那肯定不能告诉这个分布是什么~~~
聪明的你肯定先画个散点图看看大概是什么分布:
import matplotlib.pyplot as plt
plt.hist(x, bins=20)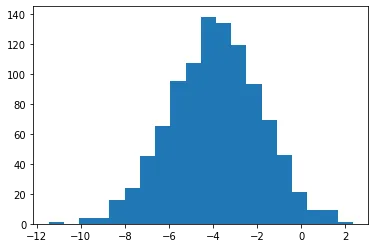
打眼一看这不就是正态分布吗,正态分布的话需要知道两个参数$\mu, \sigma$,也就是均值和标准差,于是聪明的你会定义两个变量,这两个变量就是你要learning的参数。
mu = torch.tensor(1.0, requires_grad = True)
sigma = torch.tensor(1.0, requires_grad = True)为了方便,你可能不想自己实现SGD来优化这俩参数了,你会选择使用torch内置的优化器来优化这俩参数:
optimizer = torch.optim.SGD([mu, sigma], lr=2e-2)lr是学习率,设定的小一点会好点。pytoch内置的大多数常用的分布函数,任君挑选:
q = torch.distributions.Normal(loc=mu, scale=sigma)这样就相当于定义了一个均值为1,标准差为1的正态分布$q(x)$,你的目标是通过使用最大似然估计来得到$\mu, \sigma$先写个似然函数:
negative_log_likelihood = -1 * torch.sum(q.log_prob(x_batch))pytorch并没有提供prob方法返回概率,反正你也不会用概率相乘,都是概率的对数相加,于是对log_prob求和就可以了。接下来计算$\mu, \sigma$的梯度
negative_log_likelihood.backward()
optimizer.step()顺便调用一下optimizer.step()方法来更新一下$\mu, \sigma$,执行多次之后,就能得到目标了。
至于,偷偷生成数据的过程,其实是用均值为-4,方差为2的正态分布生成了1000个样本。
于是经过上述的学习过程,$\mu, \sigma$会在-4,2前后徘徊,因为毕竟是取样的数据,与真实分布还是有差距的~
完整代码:
import numpy as np
from scipy.stats import norm
import torch
import matplotlib.pyplot as plt
# 生成数据
x = np.random.normal(loc = -4, scale = 2, size = 1000)
plt.hist(x, bins=20)
x = torch.tensor(x)
# MLE
mu = torch.tensor(1.0, requires_grad = True)
sigma = torch.tensor(1.0, requires_grad = True)
optimizer = torch.optim.SGD([mu, sigma], lr=2e-2)
# SGD
idx = list(range(len(x)))
for epoch in range(2):
np.random.shuffle(idx)
for i in range(0,len(idx),10):
x_batch = x[idx[i:i+10]]
optimizer.zero_grad()
q = torch.distributions.Normal(loc=mu, scale=sigma)
negative_log_likelihood = -1 * torch.sum(q.log_prob(x_batch))
negative_log_likelihood.backward()
optimizer.step()
print("{},{}".format(mu.detach(), sigma.detach()))